)*(Stazione Celeste)

Capitolo Tre
GEOMETRIA SACRA NEL REGNO DEI QUANTI
di David Wilcock
3.1 - I SEGRETI DI ATLANTIDE RIVISITATI
Come illustrato nel nostro precedente lavoro, una gran parte del quadro cosmologico unificato che stiamo descrivendo in questo libro è presentato con profusione di dettagli nelle scritture Vediche, che si autodefiniscono vecchie di 18.000 anni. E’ altamente probabile che l’intera cosmologia di cui stiamo ora trattando fosse già ben conosciuta nei tempi antichi sia dagli abitanti di Atlantide sia da quelli di Rama. Poi, oltre 12.000 anni fa, un cataclisma globale causò la distruzione di entrambe le civiltà. Col passare degli anni, coloro che hanno ereditato le conoscenze scientifiche hanno avuto sempre maggiori difficoltà a comprendere il “quadro generale”.
Quasi tutte le tradizioni sacre, compresa quella dei Veda, insistevano sull’esistenza di un ordine nascosto in grado di unificare tutti gli aspetti dell’Universo, e che, con sufficienti studi e visualizzazioni delle forme geometriche implicite di questo ordine, la mente dell’iniziato potesse essere connessa all’Unità dell’Universo, permettendo lo sviluppo di grandi abilità della coscienza e della mente sovrasensibile. Alcune di queste visualizzazioni hanno preso forma nello studio dei mandala come la formazione Sri Yantra. Altri hanno preferito dedicarsi a danze nelle quali il movimento e la musica erano in sintonia con questi schemi geometrici. Altri ancora si sono orientati sull’assemblare, scolpire e/o disegnare tali forme con un compasso e un righello, da cui l’importanza del principale simbolo della fratellanza Massonica, composta da una “G”, che simbolizza “Dio”[1], “Geometria e il “Grande Architetto dell’Universo”, racchiusa tra un compasso in alto e un righello in basso. Gruppi Pre-Massonici come i Cavalieri Templari hanno scelto di nascondere queste relazioni geometriche nelle loro strutture sacre, come le finestre in ferro e vetro delle cattedrali.
3.2 - GEOMETRIA SACRA E I SOLIDI PLATONICI
Dunque, la chiave di volta della conoscenza per le scuole misteriche segrete riguardo questo ordine nascosto nell’Universo è sempre stata la geometria sacra. Abbiamo parlato molto di questo argomento in entrambi i nostri precedenti libri, e incoraggiamo il lettore a fare riferimento ad essi per una più ampia comprensione. In breve, la geometria sacra è semplicemente un’altra forma di vibrazione, o “musica cristallizzata”. Consideriamo il seguente esempio:
Dapprima facciamo vibrare la corda di una chitarra. Questo crea “onde stazionarie”, cioè onde che non si muovono avanti e indietro attraverso la corda ma rimangono stabili in un posto. Vedremo alcune aree dove ci sono dei movimenti verticali estremi, che rappresentano i picchi alti e bassi dell’onda, e altre aree dove non c’è nessun movimento verticale, noti come nodi. I nodi che si formano in ogni tipo di onda stazionaria saranno sempre distanziati uniformemente l’uno dall’altro, e la velocità della vibrazione determinerà quanti nodi si formeranno. Questo significa che più alta la vibrazione sale, maggiore sarà il numero di nodi che vedremo.
In due dimensioni, possiamo sia usare un oscilloscopio sia far vibrare un “ Piatto Chladni” circolare e piano e osservare come i nodi, se uniti insieme, sviluppino forme geometriche comuni come il quadrato, il triangolo e l’esagono. Questo esperimento è stato ripetuto molte volte dai Dr. Hans Jenny, Gerald Hawkins e altri.
- Se il cerchio ha tre nodi equamente distribuiti, allora possono essere uniti per formare un triangolo.
- Se il cerchio ha quattro nodi equamente distribuiti, si può formare un quadrato.
- Se ha cinque nodi, si forma un pentagono.
- Sei nodi, un esagono, eccetera.
Sebbene sia un concetto molto semplice in termini di meccanica delle onde, Gerald Hawkins è stato il primo a stabilire matematicamente che tali forme geometriche inscritte nei cerchi fossero proprio relazioni musicali. Possiamo rimanere sorpresi nel comprendere come egli sia stato guidato a questa scoperta analizzando varie formazioni geometriche nel grano apparse nottetempo nelle campagne britanniche. Ciò è stato trattato nei nostri precedenti due libri.
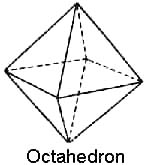
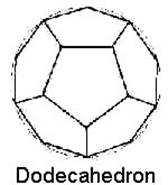
Le più profonde, riverite forme di geometria sacra sono tridimensionali, e sono conosciute come Solidi Platonici. Ci sono solo cinque formazioni esistenti che seguono tutte le regole necessarie per essere considerate tali, vale a dire l’ottaedro a otto facce, il tetraedro a quattro facce, il cubo a sei facce, il dodecaedro a dodici facce e l’icosaedro a venti facce. Qui, il tetraedro è illustrato come un “tetraedro a stella” o tetraedro intrecciato, cioè due tetraedri uniti insieme a formare una perfetta simmetria.
|
|
Figure 3.1 – I cinque Solidi Platonici di base.
Ecco alcune delle regole principali per questi solidi geometrici:
- Ogni formazione avrà la stessa forma per ogni faccia:
o Facce a triangolo equilatero nell’ottaedro, tetraedro e icosaedro
o Facce quadrate nel cubo
o Facce pentagonali nel dodecaedro
- Ogni linea di ogni formazione deve essere della stessa lunghezza
- Ogni angolo interno di ogni formazione deve essere uguale
E, cosa più importante di tutte,
- Ogni forma deve essere perfettamente inscritta in una sfera, e tutti i punti devono toccare la superficie della sfera senza sovrapposizioni.
Similmente ai casi bidimensionali riguardanti il triangolo, il quadrato, il pentagono e l’esagono inscritti nel cerchio, i Solidi Platonici sono semplicemente rappresentazioni di formazioni d’onda in tre dimensioni. Questo punto non è stato sottolineato abbastanza. Ogni punto di vertice dei Solidi Platonici tocca la superficie di una sfera nella zona dove le vibrazioni si fermano per formare un nodo. Quindi, quello che stiamo vedendo è un’immagine geometrica tridimensionale di vibrazione/pulsazione.
Entrambi gli allievi di Buckminster Fuller e del suo prediletto prof. Hans Jenny hanno escogitato esperimenti ingegnosi per mezzo dei quali mostrare come i Solidi Platonici si formino all’interno di una sfera vibrante/pulsante. Nell’esperimento condotto dagli studenti di Fuller, un palloncino sferico viene immerso nella tintura e fatto pulsare con frequenze sonore pure, conosciute come rapporti sonori “Diatonici” [2]. Un piccolo numero di nodi equidistanti si formano sulla superficie della sfera, così come le sottili linee che li connettono l’uno all’altro. Se appaiono quattro nodi equidistanti, vedremo un tetraedro. Sei nodi equidistanti formano un ottaedro. Otto nodi equidistanti formano un cubo. Venti nodi equidistanti formano un dodecaedro, e dodici nodi equidistanti formano un icosaedro. Le linee rette che vediamo su questi oggetti geometrici rappresentano semplicemente la tensione creata dalla “ distanza più breve tra due punti” nel momento in cui ognuno dei nodi si distribuisce sull’intera superficie della sfera.

Figure 3.2 – Formazione di un Solido Platonico in un fluido sferico vibrante del Dr. Hans Jenny
Il prof. Hans Jenny ha condotto un esperimento simile, una piccola parte del quale è raffigurata qui in figura 3.2, nel quale una gocciolina d’acqua contiene una sospensione molto fine di particelle colorate di chiaro, conosciuta come una “sospensione colloidale”. Quando questa gocciolina d’acqua pesantemente riempita di particelle viene fatta vibrare a varie frequenze musicali “Diatoniche”, all’interno compaiono i Solidi Platonici, circondati da linee curve ellittiche che uniscono tali nodi insieme, come vediamo in figura, dove appaiono evidenti due tetraedri nell’area centrale. Se la goccia fosse una sfera perfetta anziché una sfera appiattita, le formazioni sarebbero visibili ancor più chiaramente.
3.3 - SOLIDI PLATONICI E SIMMETRIA IN FISICA
Il mistero ed il significato dei Solidi Platonici non è ancora stato del tutto perduto dalla scienza moderna, dal momento che queste forme si adeguano a tutti i criteri necessari per creare “simmetria” in fisica in molti modi differenti. Per questa ragione, si ritrovano spesso nelle teorie che trattano della multi-dimensionalità, dove molti “piani” hanno necessità di intersecarsi simmetricamente in modo da poter essere ruotati in numerosi modi e rimanere sempre nelle stesse posizioni relative l’uno all’altro. Queste teorie multi-dimensionali includono la “group theory” (“teoria del gruppo”), conosciuta anche come “gauge theory” (“teoria del calibro”), che utilizza coerentemente vari modelli Platonici per lo spazio iperdimensionale ripiegato.
Queste stesse “funzioni modulari” sono considerate i più avanzati strumenti matematici disponibili per studiare e comprendere le “dimensioni superiori”, e la teoria delle “Superstringhe” è interamente costruita su di esse. In breve, i Solidi Platonici sono già stati riconosciuti come la chiave maestra per sbloccare il mondo delle “dimensioni superiori”. Ricordiamo che i punti precedenti sono stati menzionati in breve, essendo già stati ben trattati nei nostri precedenti libri, e che la chiave di tutto ciò è la simmetria. Quando teniamo in mente le qualità di simmetria dei Solidi di cui abbiamo parlato, le parole del Dr. Wolffs tratte dal capitolo 5 intitolato On the Importance of Living in Three Dimensions (Sull’Importanza del Vivere in Tre Dimensioni) dovrebbero assumere un particolare significato per noi:
Pag. 71 – Come vostro consigliere in esplorazione, posso dirvi che “ Ogni volta che vedete una situazione di simmetria in un problema di fisica, fermatevi e riflettete! Perché quasi sempre troverete una via più semplice per risolvere il problema usando la proprietà della simmetria”. Questa è una delle ricompense del giocare con le simmetrie. L’impressione è netta…
In matematica e geometria, c’è la necessità di essere precisi; per definizione la simmetria significa che una funzione o una figura geometrica rimane la stessa, nonostante: 1) una rotazione di coordinate, 2) una traslazione lungo un asse, o 3) uno scambio di variabili.
Nella scienza della fisica, che è il nostro argomento principale, la presenza della simmetria solitamente significa che una legge di Natura non cambia, nonostante: 1) una rotazione delle coordinate nello spazio, 2) una traslazione lungo un asse nello spazio, 3) la trasformazione del passato nel futuro quando t diventa –t, 4) uno scambio di due coordinate come per esempio x con y, z con –z, ecc., 5) lo scambio di ogni variabile data. (grassetto aggiunto)
I Solidi Platonici manifestano la più grande simmetria geometrica tra tutte le forme esistenti, sebbene qui il Dr. Wolff non le chiami per nome. Nel prossimo estratto dal dr. Aspden, egli si riferisce alle forme dei Solidi Platonici nell’etere come “cristalli fluidi”, e spiega come essi possano avere un effetto simile ad un solido, anche se compaiono in un mezzo simil-fluido:
… i fisici del 19° secolo erano in imbarazzo di fronte all’etere perché esso mostra alcune proprietà che ci dicono che è un fluido e altre che ci dicono che è un solido. Questa era la percezione in un’ epoca in cui poco o niente si conosceva dei “cristalli fluidi”. I display di molte calcolatrici tascabili usano segnali elettrici e fanno affidamento sulle proprietà di una sostanza che, come l’etere, mostra proprietà caratteristiche di entrambi gli stati liquido e solido in risposta a un’alterazione del campo elettrico.
Questo ci dà una “valida” spiegazione del perché Tesla diceva che l’etere “ si comporti come un liquido di fatto, e come un solido per luce e calore. I Solidi Platonici in realtà si comportano come fossero strutture consolidate dell’etere, organizzando i flussi energetici in schemi specifici.
Dunque: i Solidi Platonici sono semplici forme geometriche di “musica cristallizzata” che si formano spontaneamente nell’etere quando questo pulsa. Un altro punto importante da ricordare è che quando una gerarchia di Solidi Platonici evolve in un’altra, il moto avverrà sempre lungo un percorso a spirale, prevalentemente secondo il classico rapporto “phi”. E’ stato osservato che anche le Onde Torsionali seguono lo schema “phi”, cosa che sarà discussa più approfonditamente quando affronteremo il sottostimato fenomeno del “potere della piramide” e l’ “effetto della cavità strutturale” esplorato dal dr. Victor Grebennikov nel settimo capitolo.
3.4 - FISICA DEI MICROCLUSTER
Dopo aver terminato la prima metà di questo libro, un nuovo associato ci ha segnalato il germogliare del nuovo campo della “fisica dei microcluster”, che cambia interamente il nostro punto di vista sul mondo quantico, presentandoci un intero nuovo stato della materia che non obbedisce alle “regole” comunemente accettate. I Microcluster sono minuscole particelle che presentano chiare ed inequivocabili prove che gli atomi sono vortici nell’etere che si assemblano naturalmente in forma di Solidi Platonici tramite la loro vibrazione/pulsazione. Inoltre, queste nuove scoperte sono state un duro colpo per coloro che ancora credono all’esistenza di singoli elettroni orbitanti intorno ad un nucleo anziché nuvole di elettroni in forma di onde stazionarie di energia eterica assemblate in schemi geometrici. La storia dei “microcluster” irrompe per la prima volta nel mondo ufficiale nell’edizione del Dicembre del 1989 dello Scientific American, nell’articolo scritto da Michael A.. Duncan e Dennis H. Rouvray.
Dividi e suddividi un solido e i tratti caratteristici della sua solidità scompariranno uno per uno, come i tratti somatici dello Stregatto, per essere rimpiazzati da caratteristiche che comunque non sono quelle dei liquidi o dei gas. Essi appartengono invece ad un nuovo stato della materia, i microcluster… Essi pongono questioni che risiedono nel cuore della fisica e della chimica dello stato solido, e nel relativo campo della scienza materiale. Quanto piccolo deve diventare un aggregato di particelle prima che si perda il carattere della sostanza d’origine? Come possono riconfigurarsi gli atomi se liberati dall’influenza della materia che li circonda? Se la sostanza è un metallo, quanto piccolo dev’essere un gruppo (=cluster) di atomi per perdere la caratteristica condivisione di elettroni liberi che soggiace alla conduttività? (corsivo aggiunto)
Meno di due anni dopo dell’irruzione di questa storia nel mondo ufficiale, la fisica dei microcluster è stata perfezionata in un apposito testo universitario scritto da Satoru Sugano e Hiroyasu Koizumi. Microcluster Physics (Fisica dei Microcluster) è stato pubblicato dalla rispettabile, ufficiale corporazione Sprinter-Verlag come il 21° volume di una serie di testi nel campo delle scienze materiali. Tutte le citazioni tratte da questo testo che proporremo, provengono dalla seconda edizione, edita nel 1998. Nel testo di Sugano e Koizumi, ci viene detto che, con le nuove scoperte sui microcluster, possiamo ora assemblare raggruppamenti di atomi in quattro categorie base di grandezza, ognuna delle quali con differenti proprietà:
- Molecole: 1-10 atomi.
- Microcluster: 10-1000 atomi
- Particelle fini: 1000-100.000 atomi
- Massa: più di 100.000 atomi.
Studiando questa lista, ci aspetteremmo inizialmente che i microcluster posseggano tratti in comune sia con le molecole sia con le particelle fini, ma di fatto hanno proprietà che né le une né le altre mostrano, come Sugano e altri spiegano in questo passo:
I Microcluster composti dai 10 ai 103 atomi non esibiscono né le proprietà della massa corrispondente né quelle delle corrispondenti molecole di pochi atomi. Si può dire che i microcluster formino un nuovo stato della materia che è una via di mezzo tra i solidi microscopici e le particelle microscopiche come atomi e molecole, e che essi mostrino sia le caratteristiche macroscopiche sia quelle microscopiche. Comunque, le ricerche in direzione di questo nuovo stato della materia sono state lasciate intatte dallo sviluppo della teoria dei quanti della materia fino a pochi anni fa. (grassetto aggiunto)
Continuando a leggere, comprendiamo che non tutti i gruppi composti da un numero casuale di atomi compreso tra 10 e 1000 formano dei microcluster; solo alcuni “numeri magici” di atomi, unendosi, diventano effettivamente dei microcluster. Nel prossimo passo si descrive come ciò è stato scoperto per la prima volta, e mentre lo leggiamo dobbiamo tenere a mente che lo spettro di massa menzionato descrive analisi spettroscopiche, cosa che abbiamo affrontato nel capitolo precedente. Quando si parla di “strisce di cluster”, significa che atomi (come il sodio, Na) vengono estrusi attraverso un sottile becco per formare una “striscia” che viene poi analizzata. Più importante: non appena gli atomi vengono estrusi dal becco, alcuni di essi si raccolgono spontaneamente in microcluster, i quali dimostrano proprietà anomale:
Le caratteristiche microscopiche dei microcluster sono state scoperte per la prima volta osservando delle anomalie nello spettro di massa di una “striscia di cluster” di sodio (Na) di determinate dimensioni, chiamate numeri magici. Quindi è stato confermato sperimentalmente che i numeri magici provengono dalla struttura a conchiglia degli elettroni di valenza. Stimolati da queste scoperte epocali nei microcluster di metalli, e aiutati dal progresso delle tecniche sperimentali in grado di produrre microcluster relativamente densi e non interattivi[3] di varie dimensioni, in forma di strisce di microcluster, il campo di ricerca dei microcluster si è sviluppato rapidamente negli ultimi 5/7 anni [dalla prima edizione del 1991 del libro]. Il progresso si deve anche allo sviluppo dei computer e delle tecniche di calcolo computerizzato…
Il campo dei microcluster sta attirando l’attenzione di molti fisici e chimici (e anche biologi!) impegnati in ricerche sia applicate che pure, dal momento che non interessa solo i punti di vista fondamentali ma anche quelli delle applicazioni in elettronica, catalisi, ingegneria ionica, ingegneria carbon-chimica, fotografia e così via. Giunti a questo punto dello sviluppo, è stata avvertita sentita l’esigenza di un libro introduttivo per i novizi del settore, per chiarire i concetti fisici fondamentali per lo studio dei microcluster. Questo libro è destinato proprio a soddisfare tale esigenza. Ed è basato su una serie di letture fatte ai laureandi (principalmente di Fisica) dell’Università di Tokio, Università di Kyoto, Università Metropolitana di Tokyo, Tokyo Institute of Technology e Università di Kyushu, nel periodo tra il 1987 e il 1990.
La nostra prossima citazione proviene dalla prima parte del libro di Sugano e Koizumi, dove vengono presentati dettagli specifici a proposito delle proprietà altamente anomale dei microcluster. Sebbene in termini di quantità di atomi siano di poco più piccoli delle particelle fini, essi sono molto più stabili. In questo caso, la maggiore stabilità si riferisce al fatto che i microcluster bruciano a una temperatura molto maggiore delle molecole o delle particelle fini dello stesso elemento. Secondo David Hudson (del quale parleremo più avanti), gli scienziati russi furono i primi a scoprire che i microcluster dovevano essere bruciati per più di 200 secondi per far apparire uno spettro di colori analizzabile, laddove tutte gli altri composti molecolari conosciuti si consumano in un massimo di 70 secondi:
Quando dall’ulteriore divisione delle particelle fini giungiamo ad avere un frammento chiamato microcluster con un raggio dell’ordine dei 10 angstrom, osserviamo che dobbiamo prendere in considerazione una fisica differente da quella delle particelle fini. La differenza sostanziale deriva dal postulato teorico, parzialmente supportato dagli esperimenti, che, in linea di principio, sia possibile estrarre microcluster di forma e grandezza volute e che le loro proprietà possano essere misurate, mentre questo genere di misurazioni sono impossibili per le particelle fini. Questo postulato potrebbe essere giustificato considerando il fatto che gruppi di una data forma regolare sono molto stabili se comparati con quelli di altre forme, il numero dei quali è piuttosto esiguo. In contrasto con questo fatto, le particelle fini di forme differenti e di grandezza fissa che formano un grande agglomerato da permettere un trattamento statistico sono energeticamente pressoché degenerate. Ciò rende impossibile l’estrazione di particelle fini della forma voluta.
Prova definitiva si è ottenuta dal fatto che microcluster di metalli alcalini [1.8] e nobili [1.9] in forma di striscia di cluster, quando sono della grandezza dei cosiddetti numeri magici hanno una forma pressoché sferica. Un numero magico è una specifica grandezza N [cioè il numero di atomi nel cluster] dove si verificano anomalie di abbondanza negli spettri della massa. Questo indica che i microcluster di quelle dimensioni sono relativamente stabili se comparati con quelli di grandezze vicine. (grassetto aggiunto)
Nelle prossime citazioni si vedrà che le forme “pressoché sferiche” sopra citate sono proprio i Solidi Platonici e le relative geometrie. Il prossimo passaggio è probabilmente troppo tecnico per la gran parte dei lettori e può essere saltato, ma è una descrizione esaustiva di come le “strisce di cluster” vengano create e analizzate, nonché quali specifici “numeri magici” di atomi siano emersi. Inoltre, dobbiamo far notare che i cluster formati diventano elettricamente neutri, la qual cosa costituisce un altro risultato anomalo ed inatteso:
Come esempio mostriamo lo spettro di massa della striscia di cluster di Sodio della Fig. 1.5. La striscia è prodotta mediante l’espansione adiabatica di una mistura di gas di Sodio e Argon attraverso un becco. I cluster di sodio nella striscia vengono foto-ionizzati, ne viene analizzata la massa con un analizzatore di massa quadripolare, e vengono infine individuati tramite un sistema di rilevazione di ioni. Esami dettagliati dell’esperimento verificano che lo spettro di massa così osservato rispecchia i cluster [elettricamente] neutri prodotti originariamente dall’estrusione. Le anomalie di abbondanza osservate nella grandezza N, quando questa è 8, 20, 40, 58 e 93 (Fig. 1.5), fanno sì che questi vengano indentificati come i numeri magici dei cluster di Sodio neutro. (grassetto aggiunto)
Ora riponete molta attenzione alla prossima frase, perché il suo significato può essere facilmente frainteso:
In quanto segue, mostreremo che questi numeri magici sono associati con la struttura intrinseca degli elettroni di valenza che si muovono indipendentemente in un efficace potenziale a simmetria sferica…
Quello che ci viene detto è che nel microcluster gli ipotetici “elettroni” non sono più confinati nei singoli atomi di appartenenza, ma piuttosto che si muovono indipendentemente attraverso l’intero cluster stesso! Ricordate che nel nostro nuovo modello quantico, non ci sono elettroni, ma solo nuvole di energia eterica che scorrono dentro, verso il nucleo in conseguenza dell’effetto Biefield-Brown. In questo caso, il microcluster agisce come un singolo atomo, con il centro del cluster che diventa simile al nucleo atomico caricato positivamente, all’interno del quale scorre l’energia caricata negativamente. In modo interessante, tenendo a mente i comportamenti similfluidi dell’etere, il prossimo passaggio suggerisce che i microcluster possano avere proprietà simili sia ad un fluido che ad un solido:
[La simmetria dei] microcluster di metalli sembra rivelare che i microcluster appartengano al mondo microscopico come gli atomi e le molecole, laddove invece le particelle fini appartengono al mondo macroscopico. Questo è vero per certi aspetti, ma non per tutti. Nel 2° capitolo vedremo che, a temperature interne finite, i microcluster possono apparire allo stato liquido quando vengono osservati nel mondo macroscopico… (grassetto aggiunto)
Il prossimo passaggio proviene da uno studio completamente diverso di Besley ed altri, a cui si fa riferimento alla fine del capitolo, intitolato Theoretical Study of the Structures and Stabilities of Iron Clusters (“Studio Teoretico sulle Strutture e sulla Stabilità dei Cluster di Ferro”). Ovviamente, il loro lavoro si fonda direttamente sul testo di Sugano e Koizumi e sulle scoperte occorse durante la sua stesura. Qui, la chiave è che la ricerca di Besley ed altri punta sulle proprietà elettriche e magnetiche anomale possedute dai microcluster, che non si trovano né nelle molecole né nella materia condensata:
I cluster sono a buon diritto interessanti, dal momento che per piccoli cluster c’è la possibilità, nella piccola dimensione, di effetti che riconducono a proprietà elettriche, magnetiche o altro, che sono piuttosto differenti da quelle delle molecole o della materia condensata. Da un punto di vista teoretico, c’è stato anche un considerevole sforzo in direzione della ricerca per la comprensione di geometrie, stabilità e reattività di cluster di metalli puri allo stato gassoso. (grassetto aggiunto)
E ora, se saltiamo direttamente alla pag. 11 del testo di fisica dei microcluster di Sugano e altri, arriviamo alla sezione 1.3.1 intitolata Fundamental Polyhedra (=Poliedri Fondamentali). E’ qui che il collegamento tra i microcluster e la geometria della fisica di Johnson diviene chiaramente evidente:
Recentemente, si è discusso [1.12] del fatto che le forme stabili dei microcluster siano date dai 5 poliedri di Platone: tetraedro, cubo, ottaedro, dodecaedro a pentagoni, icosaedro [cioè i Solidi Platonici]; e da due poliedri di Keplero a facce romboidali; il dodecaedro e il triacontaedro romboidali…
E’ molto importante notare che i tetraedri non riempiono completamente lo spazio, come mostra la fig. 1.9, e che gli icosaedri, i decaedri trigonali e i dodecaedri pentagonali con simmetria rotazionale a cinque assi non sono strutture cristalline: essi non crescono secondo la struttura periodica della massa. Se il poliedro è una struttura non-cristallina, allora il microcluster, sulla via per diventare massa, deve sottostare a una fase di transizione verso una struttura cristallina (grassetto aggiunto)
Per chi ha studiato geometria sacra per molti anni, è sorprendente considerare che, ad un livello decisamente troppo piccolo per l’occhio nudo, gli atomi si raggruppano insieme in formazioni di Solidi Platonici perfetti. E’ anche interessante considerare che alcuni di questi microcluster possiedono anche qualità simil-fluide, per mezzo delle quali essi sono in grado di fluire da un tipo di struttura geometrica ad un’altra. Nel loro testo, Sugano e Koizumi prendono per assunto che certi poliedri come l’icosaedro e dodecaedro sono non-cristallini, e devono quindi sottostare a una fase di trasformazione prima di poter diventare un oggetto cristallizzato più grande. Comunque, più avanti in questo capitolo, presenteremo una prova forte e inconfutabile del fatto che l’intero modello della cristallografia è incompleto e che, in determinate circostanze, si possono ottenere formazioni molto simili ai microcluster a ordini di grandezza più elevati, da due o più elementi di atomi raggruppati insieme.
Se il lettore sfoglia rapidamente il resto del testo di Sugano e altri, è notevole come riesca a vedere una gran quantità di diagrammi di atomi raggruppati in Solidi Platonici. Impariamo che il raggrupparsi di un “numero magico” di atomi crea sempre una delle strutture geometriche sopra menzionate. Se prendiamo il tetraedro, per esempio, e lo smembriamo in un certo numero di sferette aventi tutte la stessa dimensione, allora avremo bisogno di un esatto “numero magico” di sferette per costruire un tetraedro di una data grandezza. E’ lo stesso modello delle “sfere chiuse” di Buckminster Fuller, e la sua forma più semplice si esprime nel fatto che se si mettono insieme tre sfere in un triangolo e poi si posiziona sopra un quarta sfera nel mezzo si otterrà un tetraedro.
Ancor più degno di nota è che alla pagina 18 del libro Microcluster Physics (Fisica dei Microcluster), Sugano riporta una fotografia di un cluster d’oro costituito da “circa 460” atomi, all’interno del quale possiamo chiaramente osservare la struttura a sfera chiusa di atomi, che forma una geometria inconfondibile. Queste immagini sono state scattate al microscopio elettronico ad alta risoluzione, e in esse è chiaramente visibile la struttura di geometria ‘cubottaedrica’ da una varietà di angolazioni diverse. Rimarchevole il fatto che si veda il cluster, immagine dopo immagine, procedere a differenti trasformazioni geometriche della propria struttura dal ‘cubottaedro’ ad altre forme, suggerendo ancora una volta qualità simil-fluide e invisibili linee di tensione dell’etere all’opera. La figura 3.3 è un diagramma che riproduce artisticamente come il numero magico di 459 atomi sferici si compattino per formare un cluster di forma ‘cubottaedrica’, mentre 561 atomi si raggruppino in forma di icosaedro.

Figura 3.3 – Cluster cubottaedrico di 459 atomi (a sinistra) e cluster icosaedrico di 561 atomi (a destra)
La prossima citazione proviene dalla sezione 3 dello studio di Besley ed altri, e propone il modello “gelatinoso” rendendo estremamente chiaro il fatto che in un microcluster la natura individuale dell’atomo si perda in favore di un comportamento di gruppo. Vedremo ancora menzionati i numeri magici e gli elettroni che si muovono attraverso l’intera struttura invece che attraverso i loro atomi di appartenenza; vedremo anche l’ipotesi che in qualche modo nei microcluster si formino “gusci geometrici” di elettroni.
Per piccoli cluster di metalli semplici, come quelli alcalini, studi spettroscopici della massa hanno indicato la presenza di nuclearità (=condizioni del nucleo) preferenziali o “numeri magici” corrispondenti a picchi particolarmente intensi. Questi esperimenti portano allo sviluppo di un modello “gelatinoso” (sferico), nel quale la geometria attuale del cluster (cioè le coordinate nucleari) sono sconosciute e irrilevanti (forse perché i cluster sono fluidi e in rapida evoluzione) e si presume che gli elettroni di valenza del cluster si muovano in un potenziale centro medio sferico. Il modello gelatinoso, perciò, spiega i numeri magici dei cluster in termini di riempimento di gusci di elettroni nei cluster, che sono analoghi ai gusci di elettroni negli atomi. Per nuclearità molto più grandi (N ~ 100-1500 [atomi totali nel cluster]) ci sono oscillazioni periodiche nell’intensità dei picchi degli spettri di massa che sono stati attribuiti all’agglomerarsi dei gusci di elettroni in supergusci.
L’osservazione di lunghi tempi di oscillazione nelle intensità dei picchi negli spettri di massa di cluster molto grandi di metalli (con più di 100.000 atomi) ha portato alla conclusione che tali cluster si evolvono attraverso la formazione di gusci geometrici tridimensionali di atomi e che per tali nuclearità è più il riempimento di gusci geometrici che non di quelli atomici che conferisce ulteriore stabilità al cluster.
Certamente, l’idea di “supergusci” di elettroni suggerisce una fusione fluida di atomi a livello quantico. Inoltre, emerge che l’idea stessa di elettroni sia fallace, dal momento che il prossimo passo di Besley e altri ci dice che il modello “gelatinoso”, nel quale elettroni “materiali” riempiono “gusci geometrici”, non funziona per quelli che sono conosciuti come metalli di transizione. Dal momento che a questo punto non possono esistere elettroni individuali, Besley e C. ipotizzano l’esistenza di “esplicite forze multi-corpo angolo-dipendenti”. In breve, un modello quantico di un “cristallo fluido” etereo è essenzialmente necessario per spiegare le forze che creano i microcluster:
Per i metalli di transizione non c’è prova a livello nucleare che il modello gelatinoso regga, anche per piccole nuclearità… speriamo che un modello che introduce esplicite forze multi-corpo angolo-dipendenti (come nel modello MM [Murrell-Mottram] che abbiamo adottato) abbia miglior successo nello spiegare le preferenze strutturali dei cluster.
Se ripensiamo ai risultati di questi studi sui microcluster, non dobbiamo dimenticare che i Solidi Platonici si formano molto facilmente facendo vibrare un regione sferica di un fluido. E’ piuttosto sorprendente che gli studiosi dei microcluster non sembrano aver notato questo collegamento. La visione prevalente della meccanica quantica come un fenomeno di particelle ha una così forte presa nelle menti dei ricercatori scientifici da richiedere una dimostrazione esaustiva a proposito dei “gusci geometrici” di elettroni. La domanda chiave che deve essere posta è come e perché questa geometria si formi, e l’idea di un mezzo quantico vibrante e simil-fluido costituisce di fatto la risposta più semplice. Un microcluster è semplicemente un più grande “atomo di etere” in una forma geometrica perfetta.
3.5 - DAVID HUDSON E GLI “ELEMENTI ORMUS”
|
ELEMENTI ORMUS CONOSCIUTI |
|
|
Elemento |
Numero Atomico |
|
Cobalto |
27 |
|
Nickel |
28 |
|
Rame |
29 |
|
Rutenio |
44 |
|
Rodio |
45 |
|
Palladio |
46 |
|
Silver |
47 |
|
Osmio |
76 |
|
Iridio |
77 |
|
Platino |
78 |
|
Oro |
79 |
|
Mercurio |
80 |
Tabella 3.1 – Microcluster di Metalli o Elementi “Ormus” conosciuti nel brevetto di David Hudson
Ora introduciamo il lavoro di David Hudson, che nei tardi anni ’70 scopre una sostanza che finirà per trasformare i microcluster in una miniera d’oro nelle sue mani. Hudson spende parecchi milioni di dollari per analizzare e testare in diversi modi queste sostanze misteriose, così che nel 1989 giungerà a brevettare la sua scoperta dei microcluster chiamandoli “ORME” (Orbitally Rearranged Monatomic Elements = Elementi Monoatomici dalle Orbite Modificate). [Nelle discussioni il nome viene comunemente cambiato in elementi “Ormus” o “M-state” per non interferire con il copywright di Hudson]. Hudson mostra un’ampia conoscenza della fisica dei microcluster nelle sue letture pubblicate dai primi anni ’90, ma le sue scoperte sono più controverse di quelle trovate nel testo di Sugano & C. o di quelle di altre pubblicazioni ufficiali. Il brevetto di Hudson si concentra sulle strutture dei microcluster da lui trovate nei seguenti metalli preziosi. (A questo punto dobbiamo notare che Sugano e Koizumi hanno stabilito che sono stati trovati microcluster anche in elementi non metallici).
Secondo Hudson nell’acqua di mare si trova una varietà sconfinata di tutti i metalli che formano microcluster sopra menzionati. In maniera ancor più sorprendente, Hudson afferma che questi elementi potrebbero essere presenti sulla Terra allo stato di microcluster in quantità di più di 10.000 volte superiore che non nella loro comune forma metallica. La ricerca di Hudson dimostra che questi microcluster di metalli si trovano in molti sistemi biologici diversi, comprese molte varietà di vegetali, e che essi possono arrivare a costituire fino al 5% in peso di materia cerebrale di un vitello. Inoltre, tali microcluster agiscono come superconduttori a temperatura ambiente, possiedono qualità superfluide e levitano in presenza di campi magnetici, dal momento che nessuna forza magnetica è in grado di penetrare attraverso i loro gusci esterni. Tali qualità fisiche combaciano con le descrizioni di vari materiali tratti da tradizioni alchemiche in Cina, India, Persia ed Europa. Varie persone si sono offerte volontarie per ingerire microcluster d’oro o “oro monoatomico”, ed hanno raccontato di aver sperimentato gli stessi effetti psichici, come le trasformazioni kundaliniche, riportate nelle scritture Vediche dell’antica India.
Ancor più controverse sono le scoperte brevettate da Hudson riguardanti il riscaldamento di microcluster di iridio. Non appena il materiale viene riscaldato, si osserva un incremento del suo peso del 300% e oltre. C’è di più: non appena un microcluster di iridio viene riscaldato fino a 850° Celsius il materiale scompare fisicamente alla vista e perde tutto il suo peso. Comunque, quando la temperatura viene nuovamente ridotta, il microcluster di iridio riappare e riguadagna gran parte del suo peso originale. Nel suo brevetto, Hudson ha una tabella generata da analisi termo-gravimetriche che illustrano l’evolversi di questo comportamento.
L’idea di un materiale che aumenta di peso, poi spontaneamente perde peso e scompare completamente alla vista non è più così fuori luogo se combiniamo le scoperte di Kozyrev con le modifiche di Ginzburg alle equazioni convenzionali della relatività e le scoperte di Mishin e Aspden sulle densità multiple dell’etere. Nel primo capitolo, Kozyrev ha mostrato come il riscaldamento o il raffreddamento di un oggetto possa influire sul suo peso in modi sottili ma misurabili. Abbiamo anche visto che questi incrementi e decrementi avvengono in improvvise esplosioni “quantiche”, non in modo lento e progressivo. Il prof. Vladimir Ginzburg suggerisce che la massa di un oggetto si converta in campo puro non appena si approssima alla velocità della luce, e i dati di Mishin e Aspden suggeriscono che la massa in realtà si evolva in una densità di energia eterica più elevata.
Così, gli effetti osservati e brevettati sui microcluster di iridio in questo volume forniscono la prima grande prova dell’idea che un oggetto possa essere completamente spostato in una dimensione (o densità) di energia eterica più elevata. Nel caso del microcluster di iridio, sembrerebbe che la struttura geometrica del microcluster permetta che l’energia del calore venga imbrigliata molto più efficientemente. L’imbrigliamento delle vibrazioni di calore, poi, crea una estrema risonanza a una temperatura relativamente più bassa, portando le vibrazioni interne dell’iridio oltre la velocità della luce. (E’ plausibile che le vibrazioni interne siano già relativamente vicine alla velocità della luce prima che venga introdotta tale risonanza, grazie alla velocità alla quale l’etere fluisce attraverso il “vortice” atomico delle nuvole elettroniche negative e del nucleo positivo). Poi, quando la soglia della velocità della luce viene raggiunta, l’energia eterica dell’iridio si sposta in una dimensione più alta, causando così la sua scomparsa dalla vista. Quando la temperatura viene ridotta, l’iridio ritorna nella nostra dimensione, dal momento che le pressione che lo teneva nella dimensione superiore è stata eliminata.
3.6 - ANOMALIE NELLE FORMAZIONI CRISTALLINE
Ora che abbiamo trattato dell’anomala situazione dei microcluster, siamo pronti ad affrontare i problemi più convenzionalmente riconosciuti della formazione dei cristalli. Il comune sale da tavola è l’esempio perfetto di come due elementi diversi, sodio e cloro, possano fondersi insieme e generare un Solido Platonico, in questo caso il cubo. Due atomi di idrogeno e uno di ossigeno si uniscono in forma di tetraedro per creare la molecola dell’acqua, (che non è un cristallo allo stato liquido ma ha una molecola tetraedrica), e i cristalli di fluoro formano un ottaedro. I cristalli che si formano con queste proprietà manterranno dappertutto al loro interno lo stesso modello, e sono simmetrici. Una descrizione più tecnica è che i cristalli sono “solidi che hanno superfici (facce) piatte che si intersecano secondo angoli specifici, e sono ordinati a livello microscopico”. La nostra domanda chiave da ricordare qui dovrebbe essere: “perché i vortici di energia che sono sferici finiscono per unirsi insieme con questi angoli e schemi così geometricamente precisi?” La risposta, ovviamente, deve essere trovata nella comprensione dei Solidi Platonici come strutture di energia “armonica” nell’etere.
La definizione classica di Glusker e Trueblood di come si formino i cristalli è che essi sono prodotti da…
…un assembramento di atomi che si ripete regolarmente. Ogni cristallo può essere visto come costituito dalla continua e ripetuta traslazione tridimensionale di un qualsiasi schema strutturale di base. (grassetto aggiunto)
Il termine “traslazione” significa ruotare un oggetto specifico di un preciso numero di gradi, come ad esempio 180°, il che formerebbe un cristallo “a due direzioni” dal momento che ci sono due traslazioni di questo tipo in un angolo giro di 360°. Così, “una traslazione ripetuta” significa che l’elemento strutturale di base (atomo o gruppi molecolari di atomi) che forma un cristallo può essere ruotato allo stesso modo più e più volte per formare lo schema ripetuto. Il termine tecnico per un accomodamento così regolare è periodicità, che significa che un cristallo è fatto di una “qualsiasi unità strutturale di base che si ripete infinitamente in tutte le direzioni, che riempie tutto lo spazio” al proprio interno. La stessa struttura (atomo o gruppo di atomi) continua a ripetersi nella stesso, periodico, modo; da cui il termine periodicità.
Nella teoria classica della formazione “periodica” del cristallo, ogni atomo conserva la propria forma e dimensione originale e non influenza gli altri atomi a parte quelli ai quali è direttamente collegato.
E’ importante comprendere che il modello della periodicità ha funzionato molto bene in cristallografia. Ogni tipo di cristallo scoperto potrebbe essere analizzato con questo metodo, e gli angoli tra le sue facce potrebbero essere predetti in base a semplici principi geometrici. In più, nel 1912, Max Von Laue scoprì un modo per utilizzare i raggi X per illuminare la struttura interna dei cristalli, creando quello che viene chiamato come “diagramma di diffrazione”. Il diagramma appare come un assembramento di singoli punti di luce su uno sfondo scuro. Questo fatto portò ad una intera scienza di ‘cristallografia a raggi X’ che fu formalizzata da William H e William L. Bragg, dove i punti di luce vengono analizzati geometricamente in relazione l’uno all’altro al fine di determinare cosa realmente sia la struttura di un vero cristallo. Nei settant’anni successivi a questa scoperta, ogni diagramma di diffrazione che è stato analizzato dagli scienziati della scienza ufficiale si adattava perfettamente al modello della periodicità, cosa che portò all’inevitabile ed apparentemente semplice conclusione che i cristalli fossero un assembramento di singoli atomi in unità strutturali.
Uno delle regole più puramente matematiche del modello della periodicità è che un cristallo può avere solo rotazioni (traslazioni) in 2, 3, 4 e 6 direzioni. In questo modello, se si ha un cristallo che è effettivamente fatto di singoli atomi o molecole in una struttura periodica ripetitiva, il cristallo non può avere una rotazione a 5 sensi o una rotazione in più di 6 direzioni. “Si suppone” che gli atomi mantengano le loro proprie identità puntiformi e che non si uniscano con altri atomi in un intero più grande. Tuttavia, in termini puramente geometrici, il dodecaedro ha cinque assi di simmetria e l’icosaedro ha 5 e 10 assi di simmetria. Questi Solidi Platonici soddisfano tutti i requisiti per la simmetria, come sottolineato dal dr. Wolff precedentemente in questo capitolo, ma non si può semplicemente impacchettare singoli atomi per creare una di queste forme. Quindi il dodecaedro e l’icosaedro hanno la simmetria ma ancora non hanno la periodicità delle formazioni cristalline. Perciò, non c’era nessun indizio in scienza che facesse credere che entrambe queste forme potessero comparire come strutture molecolari cristalline, era “impossibile”. O almeno così credevano loro…..
Ora addentriamoci nell’infame incidente di Roswell. Secondo l’ex impiegato di Groom Lake / Area 51 Edgar Fouche, sui resti rinvenuti sono state trovate delle strutture molecolari che non soddisfano il modello convenzionale della periodicità cristallina. Questi vennero conosciuti come “quasi-cristalli” (quasi-crystals), abbreviazione di “cristalli quasi-periodici” (quasi-periodic crystals) Sia l’icosaedro sia il dodecaedro apparvero in queste leghe uniche. Simili a microcluster ma ad un più elevato ordine di grandezza, questi quasi-cristalli manifestavano molte strane proprietà, come estrema durezza, estrema resistenza al calore e non-conduttività elettrica, anche se normalmente i metalli presenti in queste formazioni sono dei conduttori! (Questo concetto sarà chiarito nelle prossime righe). Diversamente dai microcluster, che pare si possano formare individualmente solo da “strisce di cluster”, i quasi-cristalli possono essere raggruppati insieme per formare delle leghe. Fouche afferma quanto segue sul proprio sito internet, con il grassetto aggiunto da noi:
Ho detenuto cariche all’interno della USAF [l’Aeronautica Militare USA] che richiedevano che fossi in possesso di accessi Top Secret, Top Secret-Crypto e di classe “Q”…
Nella sala centrale a Groom [base top secret di Groom Lake], ho udito parole come Forze di Lorentz, detonazioni pulsanti, radiazione ciclotroniche, generatori di campo a trasduzione di flusso quantico, lenti di energia di quasi-cristalli e ricevitori quantici EPR. Mi hanno detto che i quasi-cristalli erano la chiave [d’accesso] ad un intero nuovo ramo di tecnologie per la propulsione e le comunicazioni.
A tutt’oggi sono oggetto di forti pressioni affinché spieghi le eccezionali proprietà elettriche, ottiche e fisiche dei quasi-cristalli e il perché tali ricerche vengano secretate…
Quattordici anni di ricerche sui quasi-cristalli hanno permesso di stabilire l’esistenza di una ricca varietà di quasi-cristalli stabili e meta-stabili con cinque, otto, dieci e dodici assi di simmetria, con strane strutture [come il dodecaedro e l’icosaedro] e interessanti proprietà. Si è reso necessario sviluppare nuovi strumenti per lo studio e la descrizione di questi straordinari materiali.
Ho scoperto che ricerche segrete hanno mostrato che i quasi cristalli sono molto promettenti come materiali per lo stoccaggio di grandi energie, componenti di matrici metalliche, barriere termiche, rivestimenti inusuali, sensori ad infrarossi, applicazioni laser ad alta potenza ed elettro-magneti. Alcune leghe ad alta resistenza e alcuni strumenti chirurgici sono già sul mercato. [Nota: Wilcock è stato personalmente informato nel 1993 che il Teflon e il Kevlar sono entrambi frutto di retro-ingegneria]
Una delle storie che mi sono state raccontate più di una volta era che una delle coppie di cristalli usate nella propulsione dell’incidente di Roswell fosse un Cristallo di Idrogeno. Fino a poco tempo fa, creare un cristallo di idrogeno andava oltre le nostre conoscenze scientifiche. Ora la situazione è cambiata. In un Programma Black Top Secret, sotto la DOE, è stato scoperto un metodo per produrre cristalli di idrogeno, poi la produzione è iniziata nel 1994.
Il lattice di quasi-critalli di idrogeno, e un altro materiale non nominato, formavano le basi per la propulsione a scudo plasmatico del velivolo di Roswell ed era una parte integrante del motore bio-chimico del veicolo. Una quantità di avanzata cristallografia che gli scienziati non osavano nemmeno sognare fu scoperta da scienziati ed ingegneri che valutarono, analizzarono e tentarono di risalire per retro-ingegneria alla tecnologia che si era presentata col veicolo di Roswell e con altri otto veicoli che caddero dopo di allora.
Discutibilmente, dopo 35 anni di segrete ricerche sui materiali di Roswell, coloro che avevano recuperato queste tecnologie hanno ancora centinaia se non migliaia di enigmi irrisolti su quanto hanno trovato, ed è stato giudicato “prudente” introdurre i “quasi-cristalli” nel mondo non scientifico con una certa gradualità. Ora ci sono letteralmente migliaia di riferimenti diversi ai quasi-cristalli su Internet, completamente privi di ogni menzione ai microcluster. (Non un singolo studio scientifico tra quelli che siamo stati in grado di trovare in rete menziona i quasi-cristalli e i microcluster nello stesso documento). Molti dei riferimenti ai quasi-cristalli provengono da compagnie che sono partner del governo, ed è facile intuire come vengano studiati in modo intenso ed ampio. Tuttavia, non vengono quasi mai menzionati sui media generalisti, e nonostante ciò presentano una sfida unica alle nostre prevalenti teorie della fisica quantica. La ricerca va avanti, ma con una esaltazione molto dimessa.
Dan Schechtman è stato insignito dell’onere/onore di aver scoperto (o di aver avuto la possibilità di ri-scoprire) i quasi-cristalli l’8 Aprile 1982 con una lega Alluminio-Manganese (Al6Mn) che all’inizio era allo stato di liquido fuso e che poi veniva raffreddata molto velocemente. Si è verificata la produzione di cristalli in forma di icosaedro, come determinato dal diagramma a diffrazione che è stato osservato, simile all’immagine qui sotto. I dati di Schechtman non sono mai stati pubblicati fino al Novembre 1984! Nell’immagine a destra della figura 3.4 possiamo vedere chiaramente un numero di pentagoni, che indica la simmetria a cinque assi dell’icosaedro:


Figura 3.4 – L’Icosaedro (a sinistra) e il suo diagramma a diffrazione a raggi X di un quasi-cristallo (a destra)
Come abbiamo detto, con l’avvento dei quasi-cristalli, sono apparsi sia il dodecaedro che l’icosaedro, insieme ad altre inusuali forme geometriche, che in qualche modo completano la comparsa di tutti e cinque i Solidi Platonici nel mondo molecolare. Sia il dodecaedro che l’icosaedro posseggono elementi di simmetria a cinque assi con le loro strutture pentagonali. La figura 3.5 di An Pang Tsai del NRIM di Tsukuba, Giappone, mostra una lega quasi-cristallina di Alluminio-Rame-Ferro in forma di dodecaedro e una lega di Alluminio-Nichel-Cobalto in forma di prisma decagonale (10 lati):

Figure 3.5 – Prisma dodecaedrico (sin.) e decagonale (des.) di quasi-cristalli creati da An Pang Tsai del NRIM.
Il problema, qui, è che non si possono creare tali cristalli usando singoli atomi uniti insieme, ma, come possiamo ancora vedere nelle fotografie, essi sono assai reali. Il problema chiave per gli scienziati, allora, è come spiegare e definire il processo per mezzo del quale si formano questi cristalli. Secondo A.L. Mackay, uno dei modi per includere la simmetria a cinque assi nella definizione cristallografica è “l’abbandono dell’atomicità”.
Strutture frattali con cinque assi ovunque richiedono che vengano abbandonati gli atomi di grandezza finita. Questo non è un assunto realistico per i cristallografi del mondo, ma i matematici sono liberi di esplorarlo. [grassetto aggiunto]
Ciò che questo suggerisce è che, similmente ai microcluster, pare che i quasi-cristalli non abbiano più atomi individuali, ma piuttosto che gli atomi si siano fusi insieme in una unità attraverso l’intero cristallo. Mentre può apparire impossibile da credere per i cristallografi, in realtà è tra le quattro più semplici potenziali soluzioni al problema di A. L. Mackay, poiché include la semplice geometria tridimensionale e si correla con le nostre osservazioni sui microcluster. Ancora: dal momento che i cristalli sono molto reali, l’unico grande ostacolo da superare è la nostra fissazione sulla credenza che gli atomi siano fatti di particelle.
Un altro esempio a riguardo si ha nel Condensato di Bose-Einstein, teorizzato per la prima volta nel 1925 da Albert Einstein e Satyendranath Bose, e dimostrato per la prima volta in un gas nel 1995. In breve, un Condensato di Bose-Einstein è un grande gruppo di atomi che si comporta come se fosse una particella singola, con ogni atomo che lo compone che sembra occupare simultaneamente tutto lo spazio e tutto il tempo attraverso l’intera struttura. Si misura che tutti gli atomi vibrano alla stessa esatta frequenza e viaggiano alla stessa velocità, e tutto appare essere situato nella stessa area di spazio. Le varie parti del sistema agiscono rigorosamente come un intero unificato, perdendo ogni segno di individualità. Questa è la vera proprietà richiesta a un superconduttore per esistere. (Un superconduttore è una sostanza che conduce elettricità senza perdita di corrente).
Tipicamente, un condensato di Bose-Einstein può essere formato solo a temperature estremamente basse. Tuttavia, sembra di osservare un processo simile a quello che avviene nei microcluster e nei quasi-cristalli, dove non esiste più un senso di identità atomica individuale. Sorprendentemente, un altro processo simile avviene anche nella luce laser, conosciuta come luce “coerente”. Nel caso del laser, l’intero fascio di luce si comporta come se fosse un unico “fotone” nello spazio e nel tempo; in un fascio laser non c’è nessun modo per separare fotoni individuali. E’ interessante notare che i laser, i superconduttori e i quasi-cristalli sono stati tutti trovati in tecnologie ET recuperate dal 1940 in poi.
Tutto questo ovviamente introduce un intero nuovo mondo di fisica quantica sul tavolo della discussione. Nel tempo, pare che i quasi-cristalli e il condensato di Bose-Einstein saranno usati molto più diffusamente e compresi come esempi di come siamo stati fuori strada nel nostro pensiero dei quanti basati su “particelle”. Inoltre, il fisico britannico Herbert Froehlich ha supposto nei tardi anni ’60 che sistemi viventi si comportano frequentemente come i condensati Bose-Einstein, suggerendo che sia in atto un ordine a scala più alta. Discuteremo di questo nei capitoli successivi, che si accordano con la biologia eterica.

Figura 3.6 – Tavola geometrica degli Elementi di Sir William Crookes nella ristampa di Dan Winter
La nostra prossima domanda riguarda le nuvole di elettroni che sono state osservate nell’atomo. Rod Johnson e Dan Winter hanno entrambi notato che nell’atomo le nuvole di elettroni a forma di lacrima si adattano perfettamente alle facce dei Solidi Platonici. Winter si riferisce alle nuvole di elettroni come “coni a vortice” (vortex cones), e la figura 3.6 è sfortunatamente una copia illeggibile della Tavola Periodica degli Elementi come originariamente ideata da Sir William Crookes, uno scienziato famoso e altamente rispettato dei primi del ‘900, il quale in seguito divenne investigatore nel campo della parapsicologia. Nella parte bassa dell’immagine, vediamo un’illustrazione di come i “coni a vortice” si adattino su ogni faccia dei Solidi Platonici.
(Pare che una copia più leggibile della figura 3.6 esista in uno dei libri precedenti di Winter. Alcuni dei nomi degli elementi possano essere ricavati guardando l’immagine a grandezza naturale, e altri possano essere dedotti dalla loro posizione in relazione alla classica Tavola Periodica degli Elementi. Il documento ovviamente si legge dall’alto in basso, e il primo elemento che è scritto proprio sotto i due cerchi al centro è l’Elio, e la linea poi si muove verso l’elemento successivo. La scala sulla sinistra è una serie di misure graduate, che inizia dallo 0° della linea superiore e aumenta di unita di 10° per ogni linea. I numeri dei gradi scritti sulla scala sono 50, 100, 150, 200, 250, 300, 350 e 400. Questo pare indicare che la teoria di Sir Crookes comprendesse rotazioni angolari o traslazioni degli elementi in base alla loro geometria quando ci muoviamo da un elemento al successivo. Possiamo vedere che l’onda è per lo più dritta, ma al tempo stesso ci sono inclinazioni nella linea che sembrano corrispondere a rotazioni angolari più ampie che devono essere fatte).
Ritornando ai Solidi Platonici nell’etere, Aspden afferma che essi agiscono come “cristalli fluidi”, cioè che si possono comportare come solidi e come liquidi allo stesso tempo. Così, dopo aver capito che le nuvole di elettroni sono tutte posizionate secondo il modello dei Solidi Platonici, diventa molto più facile capire come si formino i cristalli e anche come probabilmente si formino i quasi-cristalli. Ci sono “nidi” di Solidi Platonici nell’atomo, un solido per ogni sfera principale nel “nido”, proprio come ci sono “nidi” di nuvole elettroniche a differenti livelli di valenza tutti co-esistenti. I Solidi Platonici formano una griglia e una struttura energetica attraverso cui l’energia eterica deve fluire non appena si avvicina al centro positivo di bassa pressione dell’atomo. Così, vediamo che ogni faccia dei Solidi funziona come un tunnel attraverso cui l’energia deve passare, creando ciò che Winter ha chiamato “coni a vortice”.
Ora che il necessario contesto è stato chiarito, i concetti di Johnson sulla simmetria Platonica all’interno della struttura di atomi e molecole del prossimo capitolo non dovrebbero risultarci così strani come probabilmente appaiono alla maggior parte delle persone. Dato quello che abbiamo visto nell’estesa ricerca che è stata sviluppata, specialmente con l’ingegneria dei quasi-cristalli, pare che questa informazione sia già sfruttata dall’umanità in certi circoli ristretti.
RIFERIMENTI:
1. Aspden, Harold. Energy Science Tutorial #5. 1997. URL: http://www.energyscience.co.uk/tu/tu05.htm
2. Crane, Oliver et al. Central Oscillator and Space-Time Quanta Medium. Universal Expert Publishers, June 2000, English Edition. ISBN 3-9521259-2-X
3. Duncan, Michael A. and Rouvray, Dennis H. Microclusters. Scientific American Magazine, December 1989.
4. Fouche, Edgar. Secret Government Technology. Fouche Media Associates, Copyright 1998/99. URL: http://fouchemedia.com/arap/speech.htm
5. Hudson, David. (ORMUS Elements) URL: http://www.subtleenergies.com
6. Kooiman, John. TR-3B Antigravity Physics Explained. 2000. URL:http://www.fouchemedia.com/Kooiman.htm
7. Mishin, A.M. (Levels of aetheric density) URL: http://alexfrolov.narod.ru/chernetsky.htm
8. Winter, Dan. Braiding DNA: Is Emotion the Weaver? 1999. URL: http://soulinvitation.com/braidingDNA/BraidingDNA.html
9. Wolff, Milo. Exploring the Physics of the Unknown Universe. Technotran Press, Manhattan Beach, CA, 1990. ISBN 0-9627787-0-2. URL: http://members.tripod.com/mwolff
[1] in inglese God=Dio, (N.d.T.)
[2] In acustica musicale, si definisce diatonica una scala ottenuta mediante la divisione dell’ottava in 5 toni e 2 semitoni. Wilcock si riferisce ai suoni diatonici come puri in quanto i loro rapporti numerici (considerati nella scala naturale) si approssimano all’intero. (N.d.T.)
[3] Ossia inerti (N.d.T.)
* * * * * * * * * *
Originale in inglese: http://www.divinecosmos.com/index.php?option=com_content&task=view&id=97&Itemid=36
Tradotto da Mauro Carfi e Andrea Calabrese per Stazione Celeste